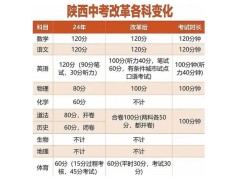
西安中考改革:化学、生物、地理“下线”,体育成“主科级
2025-10-13很多人都分不清驻点和极值点,凹凸性和拐点也搞不懂。在高等数学中,如何求函数的凹凸性和拐点问题常常令人头疼,蜂考建议先把函数的单调性和单调区间相关知识弄懂。
解决凹凸区间和拐点的方法如下:
①求出函数一阶导。
②求出函数二阶导。
③求拐点,令二阶导数等于0,在二阶导数零点处右极限异号。
④二阶导数大于0,凹区间,反之凸区间
蜂考通过经典例题为大家讲解如何求函数的凹凸区间和拐点
什么是凹凸区间和拐点?怎么求函数的凹凸性和拐点?1.1 万播放 · 7 赞同视频
驻点和极值点又如何区分,跟着蜂考继续学习吧!
一、定义
极值点:若一个函数的某一点存在某一邻域,在该邻域内函数处处都有定义,而该点的函数值为最大(小),则该函数在该点处的值就是一个极大(小)值。如果它比邻域内其他各点处的函数值都大(小),它就是一个严格极大(小)值。该点就相应地称为一个极值点或严格极值点
。
驻点:函数的一阶导数为0的点。对于多元函数,驻点是所有一阶偏导数都为零的点。二、性质不同
1、在驻点处的单调性可能改变。在极值点的左右,函数的增减性不一样,比如说在极值点的左方邻域内函数单调增加,则在极值点的右方邻域内函数单调减小。
2、驻点:一阶导数为零的点。
3、驻点关注的是,一阶导数的值为0,不关注函数的单调性变化。
极值点关注的是函数的单调性变化,不关注一阶导数是否一定存在。三、特征不同
1、极值点不一定是驻点。如y=|x|,在x=0点处不可导,故不是驻点,但是极(小)值点。
2、驻点也不一定是极值点。如y=x³,在x=0处导数为0,是驻点,但没有极值,故不是极值点。
3、可导函数极值点一定是驻点
你分得清驻点和极值点吗?1.9 万播放 · 16 赞同视频