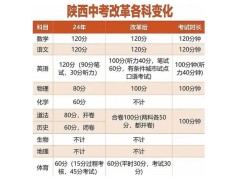
西安中考改革:化学、生物、地理“下线”,体育成“主科级
2025-10-13一、说整卷评析
试题整体结构与2022年完全一致,8道选择,5道填空,13道解答,彰显数学试题的延续性。但在考查方式和侧重点上,谋求变化。如13题由去年的菱形载体转化为矩形载体,由定量考查转换为变量考查;17题尺规作图由一次基本作图变化为两次基本作图;圆避开了与切线相关问题等,体现考查方式的变化与创新。另外,增强了对学生计算能力的考查,除了14、15、16三道考查基本运算之外,统计题中平均数的计算,圆中线段长度的分割计算,以及压轴题中最值计算,都较往年繁杂,需要较强的计算能力才能应对。纵观整套试题,稳中有变,既凸显基础,重视数学核心内容的考查;又注重数学思辨,重视思维能力、动手能力的考查;试题落地双减,非常有效地体现义务教育阶段数学的基础性、综合性、应用性、发展性及选拔性。真正体现了“三会”的核心素养育人理念。二、说考点分析
1、突出数学基础,回归课本习题试卷突出对四基的考查,没有偏怪题,落实了双减下的重基础、回归课本教育理念。如:1-8,9-12,14-19,20-25题都是常规题,是九年级复课中反复讲、练、考的基本题型,再如:26题压轴题源自课本,这类问题是八下课本P90第三章复习题第18题(1)的变式。2、立足课标,稳中有变,突出对学生核心素养的培养从重点题型来看三角形、概率、方程、一次函数、二次函数、测高、几何作图等试题考查的重难点没有太大变化。第8题考查的是二次函数求最值,全面考查了二次函数的图象与性质,出题思路较为常规,难度和2022年基本持平;13题,题目新颖灵活,有一定的难度,可以从多角度去思考本题的思维逻辑。在确定的大背景下,三个动点有两个直接的约束关系,一般来说是多解的,但是本题恰好给了"神奇"的数据,来求定值,充分考查学生分析问题和解决问题的能力;24题圆的第(2)问有一定的难度,考查的知识点有圆周角定理的推论、解直角三角形、三角形相似的应用等,综合性较强,学生准确完成有一定的困难。解决此题的关键是正确添加辅助线,充分体现了对学生运算能力、几何直观、推理能力的考查;25题二次函数的综合题在2019年考查过相关内容,但此次题目更加注重学生分析相似的类型与条件。试卷整体注重现实问题,重视对学生应用意识和能力的考查,注重对数学抽象、空间观念、推理能力、运算能力、模型思想和数据分析观念等核心素养的落实。3、突出实际情境,弘扬优秀传统文化和地方特色,增强试题灵活性关注数学在生活中的应用,用数学知识解决生活中的问题,一直是陕西中考数学命题的一大特色,如第7题以陕西特色美食“老碗面”的“老碗”为背景,21题测量景观灯的高度,22题探究树高与胸径的关系,23题“校园农场”中统计西红柿植株上西红柿的个数,25题图书楼抛物线型拱门的设计。这些试题设置新颖,来源于实际生活,让学生在答题的过程中既感受到耳目一新又觉得似曾相识。4、注重探究,突出对学生关键能力的考查如26题,考查的是"两条动线段+定长线段"最值问题,属于"过天桥"问题。本题数学思想:转化思想。解决方法:平移法通过定长线段构造平行四边形,从而达到"平移其中一条动线段"的目的。数学知识:三角形三边关系和两点之间线段最短及图形平移的综合运用。打破了考查最值问题的固有模式,以学生比较熟悉的几何图形:等腰三角形、矩形、圆、五边形为载体,问题的设计具有一定的层次性,开放性和探究性。通过这种创新和变化,再次提醒师生要更加注重基础知识、基础技能、基本思想方法、基本活动经验的落实和稳固,只有立足核心素养,夯实基础,才是关键。三、说教学启示
(一)重视教材,回归基础纵观今年的试题更多回归课本,中考备考时教师要做到对初中六册课本心中有数,吃透教材,并对课本知识进行整合,选取典型例题和课后习题再设计。七、八年级数学教师在教学中也应有中考意识,研读《课程标准》和历年中考题,并在教学中要有发展的眼光,注重基础知识的生成,对习题再设计进行变式训练,每次设计能有意识引导学生再向前一小步。如今年中考试题第20题一元一次方程的应用,就在北师大版七年级上册149页练习中可见同类题型。教师在讲本节课时,可以将题目进行改编,设计不同的背景,也可以让学生自己根据题型编题,这样不仅巩固了新知,还让学生学会灵活审题,增强了解题能力,效果可想而知。教师在中考复习时更不能犯经验主义,根据往年中考题题位进行单一复习,这样做题型若稍微变化就可能让学生无所适从。(二)解决生活问题,落实数学建模教学中我们会经常发现,学生的阅读能力弱,建模意识欠缺,畏惧处理应用问题,而教师为避免在课堂上利用生活实际问题引入而花费分析问题的时间,会将课本中的应用问题去掉,久而久之导致学生建模能力越来越弱。但作为数学核心素养之一的数学建模在中考中越来越受到重视。如今年的13题,从题面看没有常见的最短距离和轴对称模型,但是仔细审题,抽出数学模型会发现实质考查的是轴对称、垂线段最短和两点之间线段最短以及勾股定理,或者是解直角三角形的知识。联系教材,教师在讲解这些相关内容时,可以结合生活实际让学生动手设计模型,注重与生活实际联系,充分运用课本中大量的生活实例,也可进行改编,如设计学生测量学校的旗杆高度,有条件可以把本地传统文化、著名景点等文化进行渗透,让学生在学习数学的同时感受家乡之美。(三)重组教材,重视单元教学陕西中考试卷26道题,大多题目都涵盖两个或以上知识点,需要考生在规定时间内将知识重组、构建整合并进行正确的输出。而教师平时的教学是按课时设计,学生所学知识点是零碎的,不利于其整体知识构建,而大单元教学可以将散乱的、零碎的知识整合起来,实现深度学习。如在勾股定理单元教学中,教师可根据学生之前学习的三角形的知识,引导回顾三角形的认识过程,分别从角的角度、边的角度说一说,从一般到特殊,由等腰三角形中特殊的角对应特殊的边的关系,思考直角三角形特殊的角是否也有特殊的边,从而引入对《勾股定理》一章内容的探究。落实到课本内容为利用直角三角形的三边关系求边长、通过边判定直角三角形形状、化曲为直求最短距离、利用方程思想解决折叠问题、面积问题等,教师可以以专题的形式进行讲解,增强学生的模型意识,有利于构建整体认知、拓展延伸的思维能力。(四)同伴互助,抱团取暖不定期举行同学科年级间的听评课、教研交流等活动,抱团取暖,集中研讨。研讨时不仅要关注教师的教学过程,还要关注教师专业素养方面的语言以及课堂管理等方面,学习优点,提出建议,扬长避短,把每一位教师讲公开课的过程作为教师"磨课"的过程,变成全体教师和学生成长的过程。教研活动
教研促提升
携手共成长